June 1, 2019
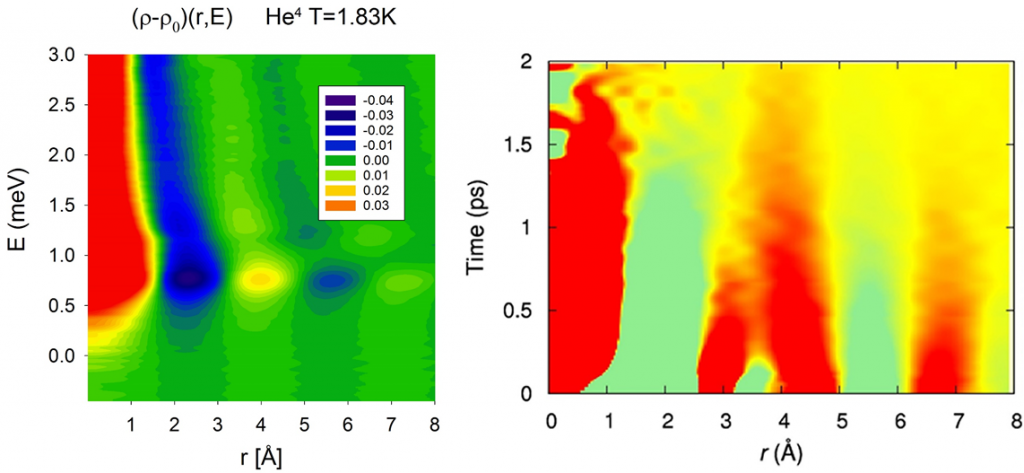
The density of a liquid is comparable to that of a solid. As you now Ice is lighter than water; otherwise the Titanic would not have gone down. Liquid is a condensed matter in which motions of atoms are highly correlated. It is challenging to figure out the atomic dynamics in liquid, and this held back the liquid state physics well behind the solid state physics. But the importance of liquid is growing, in energy storage (electrolyte), dielectrics (insulating layer in FET), and in life sciences. In solids atomic dynamics is described in terms of phonons and diffusion. But in liquids the time-scales of the two are comparable, so phonons are strongly damped and partially localized. At short-range diffusive atomic dynamics is not totally random-walk. The dynamic structure factor, S(Q, w), measured by inelastic scattering, is dominated by coherent quasi-elastic scattering, and it is not easy to interpret the results.
Our Approach
We bring the scattering data back to real space by Fourier-transforming S(Q, w) to the dynamic PDF (DyPDF), g(r, E), and to the Van Hove function (VHF), G(r, t). The DyPDF of superfluid 4He show that the atomic distances in the Bose-Einstein condensate is longer by 10% than in the non-condensate. The VHF of water show that the molecular motions in water are highly correlated, and as soon as a nearest neighbor moves away a second neighbor takes its place. From the way the VHF decays, combined with the results of molecular dynamics simulation, we determined the atomistic origin of viscosity in water. We also study the dynamics of metallic liquid alloys electrostatically levitated to avoid contact with the container, the effect of salt addition to water, organic electrolytes and nano-confined liquid. In addition, we study the mechanical properties of metallic glasses by simulation and x-ray diffraction under stress to determine the mechanism of deformation in metallic glasses.
Collaborations
ORNL; University of Tennessee, Knoxville; Washington University at St. Louis; Vanderbilt University; MIT; University of California, Berkeley; Alabama State University; Johns Hopkins University; Riken; SPring-8; The University of Tokyo